Členové: 
Alexander Lomtatidze, Zdeněk Opluštil, Jiří Šremr

Zaměření: 
Zabýváme se studiem kvalitativních vlastností řešení obyčejných diferenciálních rovnic. Jedná se zejména o otázky existence a jednoznačnosti řešení různých okrajových úloh jak v lineárním, tak i nelineárním případě a závislosti řešení na parametrech vedoucí k bifurkačním úlohám. Zajímají nás také asymptotické vlastnosti řešení obyčejných diferenciálních rovnic, např. otázky stability a oscilatoričnosti řešení. Studované rovnice jsou motivovány úlohami objevujícími se v matematických modelech procesů v mechanice a jiných inženýrských oborech, např. rovnice Duffingova typu, rovnice s relativistických diferenciálním operátorem, rovnice s \(p\)-laplacianem. Hlavním nástrojem našeho výzkumu jsou metody matematické analýzy, které jsou vhodně přizpůsobeny pro studium jednotlivých úloh. 

Spolupráce s ostatními ústavy fakulty i mimo ní: 
Jsme otevřeni jakékoli spolupráci v oblastech našeho zájmu. Pro bližší představu níže uvádíme některé úlohy, kterými se v poslední době zabýváme.
    V současné době probíhá spolupráce s Odborem fluidního inženýrství Viktora Kaplana Energetického ústavu (zejména s panem profesorem Pochylým) v otázce matematického modelovaní pulzací kapaliny v uzavřené nádobě.

Některé oblasti výzkumu, výstupy:
Členové skupiny výsledky svého výzkumu publikují v tuzemských i mezinárodních odborných časopisech a prezentují na odborných seminářích a konferencích.
   V poslední době se zabýváme zejména následujícími úlohami:

• Otázka existence, multilicity a struktury množiny všech periodických řešení neautonomní rovnice matematického kyvadla $$\small u''=p(t)\sin u+q(t),$$ kde \(\small p,q\) jsou libovolné \(\omega\)-periodické funkce lokálně lebesgueovsky integrovatelné, a jeho zobecnění pro rovnici s relativistickým diferenciálním operátorem $$\small \left(\frac{u'}{\sqrt{1-[u']^2}}\right)'=p(t)\sin u+q(t),$$ V současné době dokončujeme přípravu publikace:
  • Lomtatidze, A. On periodic solutions to relativistic pendulum-type equation.
• Principy maxima/antimaxima a jejich souvislosti se stabilitou lineární diferenciální rovnice $$\small u''+g(t)u'+p(t)u=0$$ s nekonstantními periodickými koeficienty. I když se zdá, že se jedná o velmi jednoduchou diferenciální rovnici, zmiňované vlastnosti jsou podrobně vyšetřeny pouze v případě konstantního tlumícího koeficientu \(\small g\). V případě nekonstantního tlumícího koeficientu je spousta zajímavých otázek stále otevřena.
• Existence a multiplicita kladných periodických řešení obyčejných diferenciálních rovnic Duffingova typu. Takové rovnice dostáváme běžně po aproximaci nelinearit v pohybových rovnicích různých oscilátorů pomocí Taylorových polynomů vyšších stupňů.

  

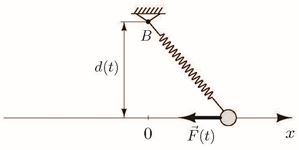
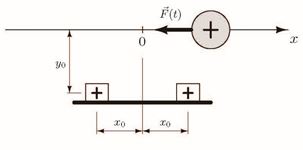
  Výsledky získané pro rovnice s nekonstantními koeficienty zobecňují vlastnosti autonomních rovnic. V autonomním případě, tj. pro rovnice s konstantními koeficienty, lze zmiňované vlastnosti odvodit vcelku lehce (např. vyšetřením chování fázových trajektorií v okolí ekvilibrií), avšak v neautonomním případě je třeba použít různé techniky kvalitativní teorie diferenciálních rovnic (věty o diferenciálních nerovnostech, horní a dolní funkce okrajové úlohy, Fredholmovy věty, Sturmovy  oddělovací a srovnávací věty atd.). Jako příklad můžeme uvést periodickou okrajovou úlohu $$\small u''=p(t)u+h(t)u^3+\mu f(t),\quad u(0)=u(\omega),\ u'(0)=u'(\omega),$$ kde \(\small p,h,f\) jsou funkce lebesgueovsky integrovatelné na intervalu \(\small [0,\omega]\) a \(\small\mu\) je reálný parametr. Některé naše výsledky o existenci a multipicitě kladných řešení této úlohy v závislosti na hodnotách parametru \(\small\mu\) lze nalézt v publikacích:
  • Šremr, J. Parameter-dependent periodic problems for non-autonomous Duffing equations with sign-changing forcing term. Electronic Journal of Differential Equations, 2023, roč. 2023, č. 65, s. 1-23. ISSN: 1072-6691.
  • Šremr, J. Bifurcation of positive periodic solutions to non-autonomous undamped Duffing equations. Mathematics for applications, 2021, roč. 10, č. 1, s. 79-92. ISSN: 1805-3610.
  Pro rovnici s \(\small\mu=0\) dokončujeme přípravu publikace:
  • Lomtatidze, A., Šremr, J. On a peridic problem for second order Duffing type equation.
• Uzavíráme řadu našich publikací týkajících se oscilatorických vlastností pololineárních soustav obyčejných diferenciálních rovnic $$\small \begin{array}{l}u'=g(t)|v|^{1/\alpha}\mathrm{sgn}\,v,\\v'=-p(t)|u|^{\alpha}\mathrm{sgn}\,u,\end{array}$$ kde \(\small p,g\) jsou funkce lokálně lebesgueovsky integrovatelné na intervalu \(\small [0,+\infty[\). Za naši úvodní publikaci v této oblasti můžeme považovat
  • Lomtatidze, A., Dosoudilová, M., Šremr, J. Oscillatory properties of solutions to certain two-dimensional systems of non-linear ordinary differential equations. Nonlinear Analysis, Theory, Methods and Applications, 2015, roč. 2015(120), č. 1, s. 57-75. ISSN: 0362-546X,
  na niž navazují publikace obsahující efektivní oscilační a neoscilační kritéria, například:
  • Opluštil, Z. On non-oscillation for certain system of non- linear ordinary differential equations. Georgian Mathematical Journal, 2017, roč. 24, č. 2, s. 277-286. ISSN: 1072-947X.
  • Opluštil, Z. Oscillatory properties of certain system of non-linear ordinary differential equations. Miskolc Mathematical Notes (electronic version), 2018, roč. 19, č. 1, s. 439-459. ISSN: 1787-2413.
  • Opluštil, Z. On non-oscillation for two dimensional systems of non-linear ordinary differential equations. Miskol Mathematical Notes. V tisku.
• Pokračujeme ve studiu oscilatoričnosti řešení lineárních diferenciálních rovnic 2. řádu s odkloněným argumentem. Techniku vytvořenou pro zpožděné rovnice v článku
  • Opluštil, Z., Šremr, J. Myshkis type oscillation criteria for second-order linear delay differential equations. Monatshefte fur Mathematik, 2015, roč. 2015 (1), č. 1, s. 143-161. ISSN: 0026-9255
  jsme přizpůsobili i pro studium diferenciálních rovnic $$\small u''+p(t)u(\tau(t))=0,$$ se zrychlenným argumentem (tj. pro případ \(\small\tau(t)\geq t\)) a získané výsledky jsou zaslány k publikaci:
  • Opluštil, Z. Oscillation criteria for the second-order linear advanced differential equations. Applied Mathematics Letters.

Bakalářské a diplomové práce:
Témata závěrečných prací jsou vypisována jak z oblasti prováděného výzkumu, tak i z oblasti aplikací diferenciálních rovnic ve fyzice a inženýrských oborech. Jsou také vypisována témata z ostatních oblastí matematické analýzy, které nejsou zahrnuty ve studijních programech a mohou tak rozšířit znalosti studentů matematického inženýrství.